Linguagens Formais e Autômatos
Linguagens Regulares e Livres de Contexto
Posts Relacionados
Conversão de Autômatos Finitos em Expressões Regulares
Na última aula vimos como transformar uma expressão regular em um automato finito, provando que as expressões regulares, no máximo, representam o mesmo tipo de linguagem reconhecida pelos automatos finitos determinísticos (as linguagens regulares). Para provar a equivalência entre os dois formalismos, é necessário que demonstremos que qualquer autômato finito determinístico possa ser transformado em uma expressão regular.
Pra facilitar a conversão do de um automato finito em uma expressão regular vamos estudar um novo conceito, Autômato Finito Não-Determinístico Generalizado (GNFA, do inglês Generalized Nondeterministic Finite Automaton).
Autômato Finito Não-Determinístico Generalizado (GNFA)
Um autômato Finito Não-Determinístico Generalizado é semelhante a um NFA, mas permite o uso de expressões regulares como símbolo de ativação das transições.
A diferença na computação de um GNFA é que ao invés de ler um único símbolo, a transição irá consumir toda uma string.
A aceitação ou rejeição de uma entrada é a mesma do NFA, se houver qualquer caminho que, ao final da entrada, levar a um estado de aceitação, a entrada será aceita, caso contrário, ela será rejeitada.
Por conveniência, vamos assumir uma forma especial do GNFA, onde:
- Existe apenas um estado de aceitação, separado do estado inicial.
- Devem existir transições de entrada e saída entre todos os estados do autômato:
- o estado inicial só possui transições de saída.
- o estado final só possui transições de entrada.
Prova da conversão GNFA em Expressões regulares
Lema: Todo GNFA $G$ tem uma expressão regular $R$ equivalente.
Prova: Por indução do número de estados $k$ de $G$.
- Base: $k = 2 : G = \rightarrow\bigcirc\overset{r}{\rightarrow}\bigodot$
- Lembre-se que $G$ está na forma especial
- $R = r$
- Passo de Indução ($k > 2$)
- Assumimos que o lema é verdade para $k-1$ estados e provar para $k$ estados.
- Ideia: Converter o GNFA de $k$ estados para o GFNA com $k-1$ estados.
- Escolher um estado qualquer $x$ que não seja o estado inicial ou o estado final.
- Remover o estado $x$.
- reconstruir todos os caminhos que passavam por $x$
- Faço o mesmo para todo par de estados $q_i, q_j$

Lema do Bombeamento
Para mastrar que uma linguagem é uma linguagem regular, é preciso contruir um DFA, ou criar a liguagem por indução utilizando os fechos de linguagens regulares.
Para mostrar que uma linguagem não é regular é preciso mostrar uma prova, e não é possível dizer que não existe um DFA para ela, pois isso não é uma prova.
Dado o alfabeto $\Sigma = \{0, 1\}$:
- Seja $B = \{w | w\; \text{tem um numero igual de 0s e 1s}\}$
- Intuição: $B$ não é regular porque DFAs não podem contar infinitamente.
- Seja $C = \{w | w\; \text{tem um numero igual de substrings 01 e 10}\}$
- $0101 \notin C$
- $0110 \in C$
- Intuição: $C$ não é regular porque DFAs não podem contar infinitamente.
- Na realidade, $C$ é regular.
- Regex: $00^{*}(11^{*}00^{*})^{*}\,|\,11^{*}(00^{*}11^{*})^{*}$
Lema do Bombeamento: Para toda linguagem regular $A$, existe um número $p$ (o tamanho do bombeamento), de tal modo que se $s \in A$ e $|s| \ge p$ então $s = xyz$ onde:
- $xy^{i}z \in A, \forall{i} \ge 0 \quad \quad \quad y^i = \underbrace{yyy\cdots{y}}_{i}$
- $y\ne\varepsilon$
- $|xy|\le{p}$
Informalmente: $A$ é regular se cada cadeia longa em $A$ pode ser bombeada e o resultado continua em $A$.
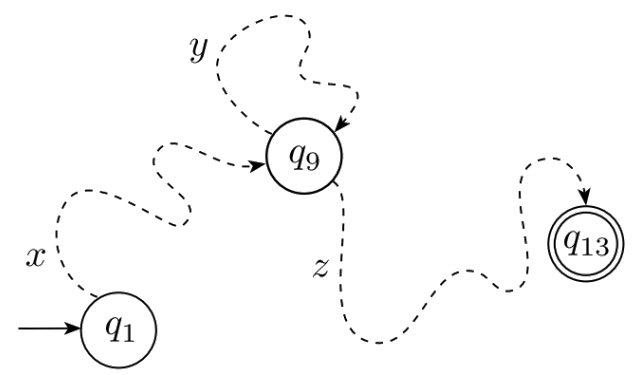
Prova: Seja $M$ um DFA que reconhece $A$, seja $p$ o número de estados em $M$, escolha $s \in A$ onde $|s| \ge p$
- $M$ vai, obrigatoriamente repetir um estado $q_j$ quando avaliar $s$, porque $s$ é muito longa.
- Logo, $xyyz$ também é aceita.
Aplicação do Lema do Bombeamento
Seja $D = \{0^k1^k | k\ge{0}\}$, demonstraremos que D não é regular por uma prova por contradição.
- Assumimos que $D$ é regular, logo podemos aplicar o lema do bombeamento.
- Pelo lema do bombeamento, dizemos que $s = 0^p1^p \in D$
- Podemos, então, divivir a cadeia, tal que $s = xyz$ satisfazendo as três condições.
- Se cortarmos de forma que $|xy| \le p$, ao criar $xyyz$, haverá um número excessivo de $0$, logo $xyyz \notin D$.
- Como esse resultado contradiz o que assumimos (que $D$ é regular), temos que assumir que $D$ não é regular.
Seja $F = \{ww | w \in \Sigma^*\}$, demonstraremos que F não é regular por uma prova por contradição.
- Assumimos que $F$ é regular, logo podemos aplicar o lema do bombeamento.
- Pelo lema do bombeamento, dizemos que $s = 0^p0^p \in D$
- Se escolhermos $y = 00$, a palavra $xyyz$ ainda estará em $F$, porém isso não prova que $E$ é regular.
- A escolha da cadeia utilizada e como ela será dividida pode ter resultados diferentes, mas basta que seja demonstrado que uma cadeia não funcione para que a linguagem não seja regular.
- Escolhemos, então, uma outra palavra $s = 0^p10^p1 \in F$
- Tentaremos, novamente, divivir a cadeia, tal que $s = xyz$ satisfazendo as três condições.
- Se cortarmos de forma que $|xy| \lt p-1$, ao criar $xyyz$, haverá um número excessivo de $0$, logo $xyyz \notin F$.
- Como esse resultado contradiz o que assumimos (que $F$ é regular), temos que assumir que $F$ não é regular.
Voltamos agora a linguagem $B = \{w | w\; \text{tem um numero igual de 0s e 1s}\}$:
- Vamos assumir, para provar por contradição, que $B$ é regular.
- Sabemos que $0^*1^*$ é regular, logo, $B \cap 0^*1^*$ é regular (fechada para intersecção das linguagens regulares).
- Como $D = B \cap 0^*1^*$ e já mostramos que $D$ não é regular, chegamos a uma contradição!
- Logo $B$ não pode ser regular!


