Linguagens Formais e Autômatos
Posts Relacionados
Conjuntos
Veja Conjuntos
Questões
- Forneça uma descrição informal para os seguintes conjuntos:
- $\{1, 3, 5, 7, \dots\}$
- $\{\dots, -4, -2, 0, 2, 4 \dots\}$
- $\{n | n = 2m \text{ para algum } m \text{ em } \mathbb{N} \}$
- $\{n | n = 2m \text{ para algum } m \text{ em } \mathbb{N} \text{ e } n=3k \text{ para algum } k \text{ em } \mathbb{N} \}$
- $\{w | w \text{ é uma cadeia de 0s e 1s e } w \text{ é igual a } w^\mathcal{R}\}$
- Forneça descrições formais para os seguintes conjuntos:
- O conjunto contendo os números 1, 10 e 100.
- O conjunto contendo todos os números inteiros que são maiores que 5.
- O conjunto contendo todos os números naturais que são menores que 5.
- O conjunto contendo a cadeia
ada - O conjunto contendo a cadeia vazia
- O conjunto contendo absolutamente nada.
- Seja $A$ o conjunto ${x, y, z}$ e $B$ o conjunto ${x, y}$
- $A$ é um subconjunto de $B$?
- $B$ é um subconjunto de $A$?
- $A \cup B =$
- $A \cap B =$
- $A \times B = $
- Qual o conjunto das partes de $A$?
- $A \subseteq B $ ?
- $B \subset A $ ?
- Se um conjunto $A$ tem $a$ elementos e um conjunto $B$ tem $b$ elementos, quantos elementos estão em $A \times B$? Explique a sua resposta.
Lógica Booleana
Veja a página sobre lógica booleana
Questões
- Duas pessoas querem jogar o jogo Pedra, Papel e Tesoura, escreva as regras do jogo utilizando operadores e operandos booleanos. (Dica: Use R para pedra, P para papel e S para tesoura.)
- Reescreva as suas regras utilizando apenas os operadores $\lnot$ e $\land$
- Reescreva as suas regras utilizando apenas os operadores $\lnot$ e $\lor$
- Dada uma expressão booleana com N operadores, quantas instâncias dessa expressão podem ser criadas?
Demonstrações
Uma habilidade importante para a vida é a capacidade de distinguir entre um argumento plausível e um argumento que está totalmente correto. Esta habilidade é um entendimento básico do que é a matemática, pois precisamos saber que é absolutamente irrefutável e inevitável, e o que é apenas muito provável.
Sabendo criar demonstrações matemáticas sobre algo nos permite não apenas criar argumentos irrefutáveis (provas), mas, muitas vezes, encontrar uma solução para um problema, ao tentar provar um hipótese sobre ele.
Prova por imagem
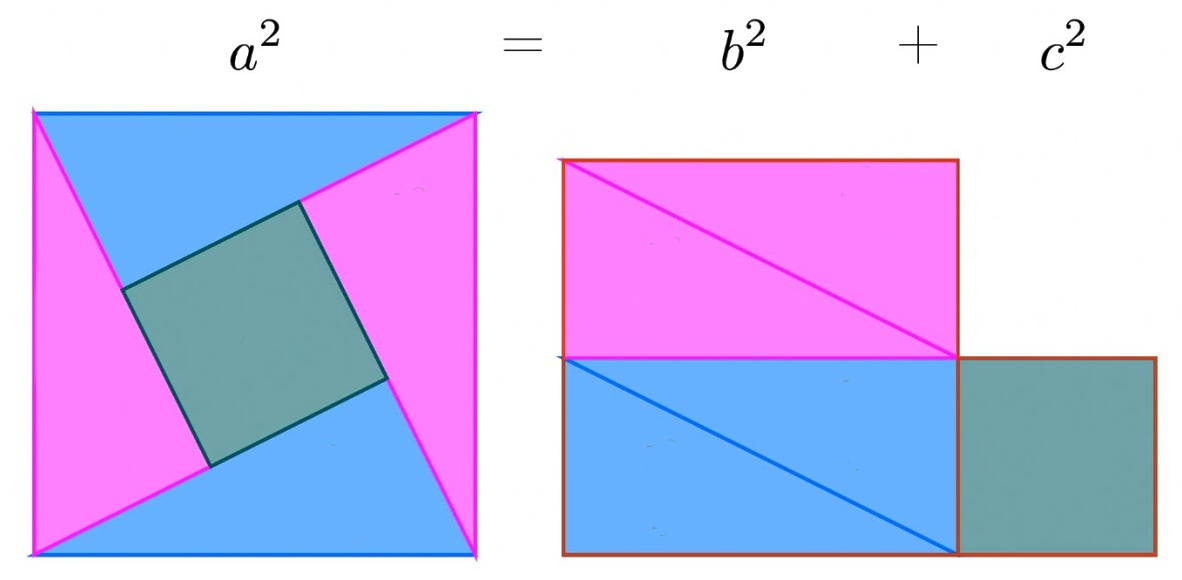
A prova por imagem é uma prova muito prática e elegante!
Porém é um tipo de prova que preocupa muito os matemáticos…

… e os matemáticos se preocupam porque existem muitas premissas que não estão claras.
Suposições ocultas podem trazer ambiguidades e ambiguidades podem trazer problemas na prova de fórmulas, por exemplo:
\[\begin{gather} 1 = -1 \\ 1 = \sqrt{1} = \sqrt{-1\times-1} = \sqrt{-1}\sqrt{-1} = (\sqrt{-1})^2 = -1 \end{gather}\]O problema de utilizar uma prova errada é que esse erro se propaga para outros casos:
\[\begin{align} 1 = -1 \\ \frac{1}{2} = -\frac{1}{2} & & (\times \frac{1}{2}) \\ 2 = 1 & & (+ \frac{3}{2}) \end{align}\]Introdução as provas formais
Por que queremos provar ou demonstar algo de maneira formal? Porque uma vez que conseguimos uma demonstração formal, correta, de um enunciado, assumimos isso como verdade e podemos, até mesmo, utilizar o enunciado em outras provas.
Uma definição descreve objetos e noções que utilizamos. Um enunciado matemático expressa que algum objeto tem certa propriedade. Tanto as definições como os enunciados matemáticos devem ser precisos, deixando claro o que constitui ou não constitui o objeto, sem ambiguidades. Enunciados podem ou não ser verdadeiros.
Uma prova é um argumento lógico convincente de que um enunciado é verdadeiro. Na matemática, um argumento precisa ser inatacável, ou seja, convincente em um sentido absoluto. Em algumas situações, como no Direito, as provas não precisam ser além de qualquer dúvida, como na matemática, basta que sejam suficientemente suportadas pelas evidências. Na matemática, as evidências não desempenham papel nenhum em uma prova.
Um teorema ´é um enunciado matemático demonstrado como verdadeiro. Geralmente utilizamos esse termo para enunciados de especial interesse. Ocasionalemente provamos enunciados que só são interessantes para a prova de outros enunciados, e chamamos esses enunciados de lemas. Quando um teorema, ou a prova dele, nos permitem concluir facilmente que outros enunciados relacionados são verdadeiros chamamos esse enunciados de corolários do teorema.
Provas por Dedução
Uma prova por dedução consiste em uma sequência de afirmações cuja verdade nos leva de alguma afirmação inicial, chamada hipótese, a uma afirmação de conclusão. Cada etapa da prova deve seguir por um princípio lógico aceito, a partir dos fatos dados, de algumas afirmações anteriores na prova dedutiva, ou de uma combinação desses elementos.
- Teorema 1: Se $x \ge 4$, então $2^{x} \ge x^{2}$
- O lado esquerdo sempre cresce duplicando o valor.
- O lado direito crsece a uma taxa de $\frac{x+1}{x}$, que no melhor caso ($x = 4$), é $1,5625$.
- Como $2 > 1,5625$, o lado esquerdo sempre crescerá a uma taxa maior que o lado direito.
- Logo, se $x\ge 4$, então $2^{x}\ge x^{2} \quad \square$
Utilizando essa prova informal do Teorema 1, podemos provar um outro teorema.
- Teorema 2:: Se x é a soma dos quadrados de quatro inteiros positivos, então $2^x \ge x^2$
| # | Afirmação | Justificativa |
|---|---|---|
| 1. | $x = a^2 + b^2 + c^2 + d^2$ | Dado |
| 2. | $a \ge 1$, $b \ge 1$, $c \ge 1$, $d \ge 1$ | Dado |
| 3. | $a^2 \ge 1$, $b^2 \ge 1$, $c^2 \ge 1$, $d^2 \ge 1$ | (2) e propriedades da aritmética |
| 4. | $x \ge 4$ | (2), (3) e propriedades da aritmética |
| 5. | $2^x \ge x \quad \square$ | (4) e Teorema 1 |
Nem sempre, os termos utilizados nos enunciados tem implicações óbvias, veja um exemplo.
- Teorema 3: Seja $S$ um subconjunto finito de algum conjunto infitino $U$. Seja $T$ o cemplemento de $S$ em relação a $U$. Então, T é infinito.
| Afirmação original | Nova afirmação |
|---|---|
| S é infinito | Existe um inteiro $n$ tal que $\norm{S} = n $ |
| U é infinito | Para nenhum inteiro $p$ temos $\norm{U} = p $ |
| T é o complemento de S | $S \cup T = U \land S \cap T = \varnothing $ |
Uma característica desejada das provas é que sejam curtas, então usando os dados anteriores, vamos provar informalmente, o Teorema 3:
Sabemos que $S \cup T = U$ e $S$ e $T$ são disjuntos, e assim $\norm{S} + \norm{T} = \norm{U}$. Como $S$ é finito, sabemos que existe um valor $n$, tal que $\norm{S} = n$. Agora, vamos supor que $T$ seja finito, ou seja, $\norm{T} = m$, então temos que $\norm{U} = \norm{S} + \norm{T} = n + m$, o que contradiz a afirmação que para nenhum inteiro $p$ temos $\norm{U} = p$, o que contradiz a suposição feita. Dessa forma, como sabemos que o tamanho de $S$ é finito, provamos, por contradição, que o tamanho de $T$ é infinito. $\square$
A prova por contradição é uma técnica para provar enunciados onde afirmamos a hipótese complementar do que queremos provar, e a provamos falsa, restando apenas que a afirmação original é verdadeira.
Exercícios
Prove informalmente, ou refute, os seguintes teoremas:
- $\sin^2 \theta + \cos^2 \theta = 1$
- Todo número primo é impar
- Não existe par de inteiros $a$ e $b$ tais que $a \bmod b = b \bmod a$
Preparação para a próxima aula
Continuaremos com o estudo de provas na próxima aula, onde veremos provas por indução, que serão muito importantes para essa disciplina. Os recursos para você se preparar para a próxima aula são os mesmos desta aula.
Alem disso, recomenda-se fortementa a execução de um ou dos dois tutoriais sobre Git, se você não sabe como utilizar o Git e o Github:
Recursos para essa aula
Bibliografia
- Capítulo 0 do livro Introdução a Teoria da Computação
- Livro do Hopcroft(físico), capítulo 1, seções 1.1 até 1.4 (inclusa).
Videos
- Aulas 1 e 2 de MIT 6.042j Mathematics for Computer Science 2010
- Videos da unidade 1, Proofs, de MIT 6.042j Mathematics for Computer Science 2019